설명
현수는 다음 달에 결혼을 합니다.
현수는 결혼식 피로연을 장소를 빌려 3일간 쉬지 않고 하려고 합니다.
피로연에 참석하는 친구들 N명의 참석하는 시간정보를 현수는 친구들에게 미리 요구했습니다.
각 친구들은 자신이 몇 시에 도착해서 몇 시에 떠날 것인지 현수에게 알려주었습니다.
현수는 이 정보를 바탕으로 피로연 장소에 동시에 존재하는 최대 인원수를 구하여 그 인원을 수용할 수 있는 장소를 빌리려고 합니다. 여러분이 현수를 도와주세요.
만약 한 친구가 오는 시간 13, 가는시간 15라면 이 친구는 13시 정각에 피로연 장에 존재하는 것이고 15시 정각에는 존재하지 않는다고 가정합니다.
입력
첫째 줄에 피로연에 참석할 인원수 N(5<=N<=100,000)이 주어집니다.
두 번째 줄부터 N줄에 걸쳐 각 인원의 오는 시간과 가는 시간이 주어집니다.
시간은 첫날 0시를 0으로 해서 마지막날 밤 12시를 72로 하는 타임라인으로 오는 시간과 가는 시간이 음이 아닌 정수로 표현됩니다.
출력
첫째 줄에 피로연장에 동시에 존재하는 최대 인원을 출력하세요.
예시 입력 1
5
14 18
12 15
15 20
20 30
5 14
예시 출력 1
2
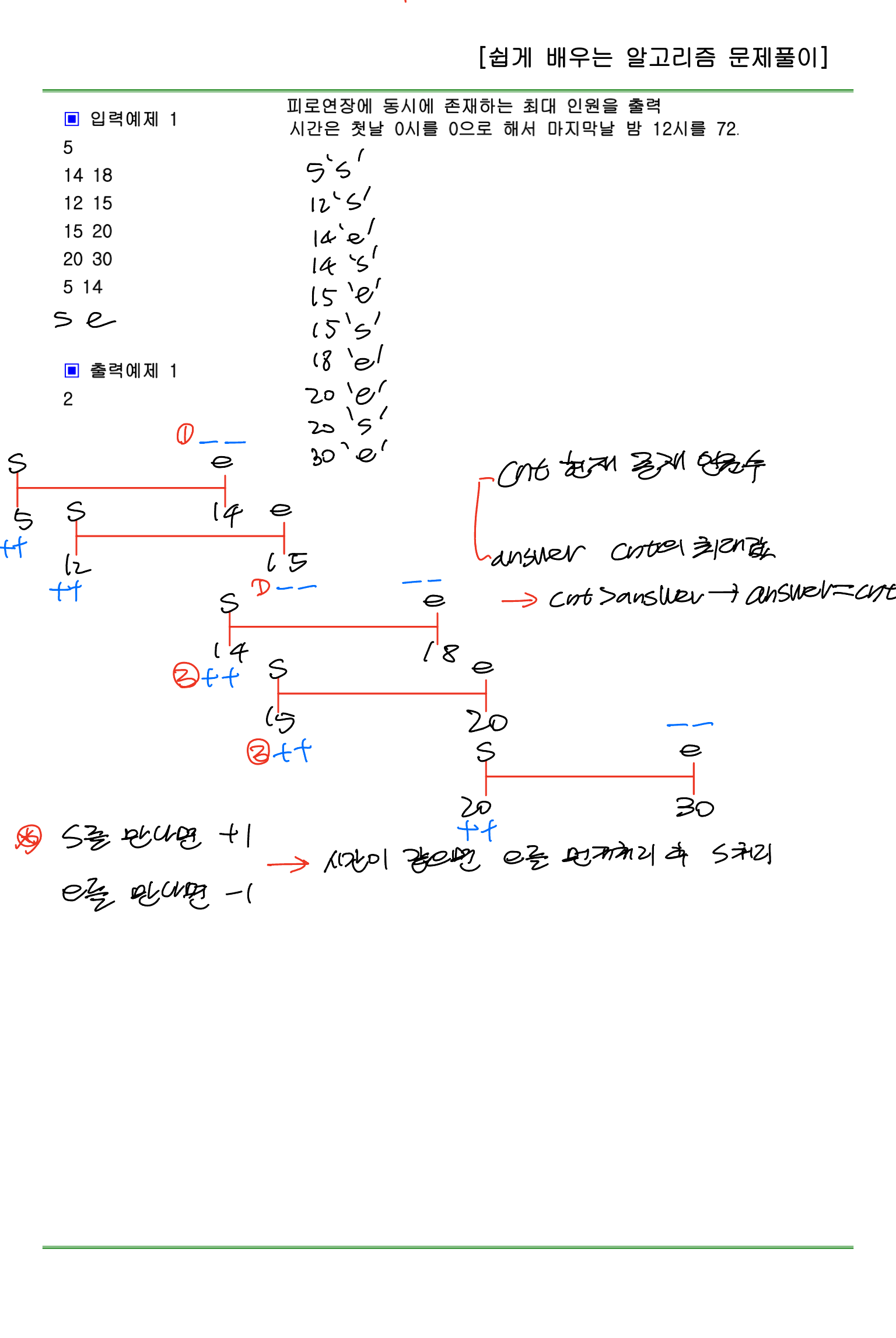
어렵게 생각하지 말고,
올바르게 정렬 후,
시작 시간일 경우 cnt++;
끝나는 시간일 경우 cnt--;
import java.util.*;
class Wedding implements Comparable<Wedding> {
char x;
int y;
Wedding(char x, int y) {
this.x = x;
this.y = y;
}
@Override
public int compareTo(Wedding o) {
// s이면 작은 순 -> y가 같으면 e먼저
if (this.y == o.y)
return this.x-o.x;
return this.y - o.y;
}
}
public class Main {
static Queue<Wedding> q = new PriorityQueue<>();
public static void main(String[] args) {
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
for (int i = 1; i <= n; i++) {
char x = ' ';
int y = 0;
x = 's';
y = kb.nextInt();
q.offer(new Wedding(x, y));
x = 'e';
y = kb.nextInt();
q.offer(new Wedding(x, y));
}
System.out.println(solution(n));
}
static int solution(int n) {
int answer = Integer.MIN_VALUE;
int cnt = 0;
while (!q.isEmpty()) {
Wedding w = q.poll();
if (w.x == 's')
cnt++;
answer = Math.max(answer, cnt);
if (w.x == 'e')
cnt--;
}
return answer;
}
}+) 세련된 풀이
import java.util.*;
class Time implements Comparable<Time>{
int time;
char state;
Time(int time, char state){
this.time=time;
this.state=state;
}
@Override
public int compareTo (Time ob){
if(this.time==ob.time){
return this.state-ob.state;
}
else
return this.time-ob.time;
}
}
public class Main {
static int solution(ArrayList<Time> arr){
int cnt=0;
int answer=Integer.MIN_VALUE;
Collections.sort(arr);
for(Time t : arr){
if(t.state == 's'){
cnt++;
}
else
cnt--;
answer=Math.max(cnt,answer);
}
return answer;
}
public static void main(String[] args){
Scanner kb=new Scanner(System.in);
int n = kb.nextInt();
ArrayList<Time> arr = new ArrayList<>();
for(int i=0;i<n;i++){
int sT=kb.nextInt();
int eT=kb.nextInt();
arr.add(new Time(sT, 's'));
arr.add(new Time(eT, 'e'));
}
System.out.println(solution(arr));
}
}#풀이 방법
1. PriortyQueue를 이용해, 들어온 시간 기준 오름차순, 시간이 같을 경우, 나가는 시간 기준으로 오름차순으로 큐를 정렬해서 풀이
2. 리스트에 Room객체를 넣고, 위와 같이 정렬시켜서, 해당 리스트를 돌면서 풀이
+) 02.22
#시간 초과
//1. 우선순위큐를 이용한 풀이
static Queue<Wedding> q = new PriorityQueue<>();
for (int i = 1; i <= n; i++) {
char x = ' ';
int y = 0;
x = 's';
y = kb.nextInt();
q.offer(new Wedding(x, y));
x = 'e';
y = kb.nextInt();
q.offer(new Wedding(x, y));
}
//2. ArrayList를 이용한 풀이
ArrayList<Time> arr = new ArrayList<>();
for(int i=0;i<n;i++){
int sT=kb.nextInt();
int eT=kb.nextInt();
arr.add(new Time(sT, 's'));
arr.add(new Time(eT, 'e'));
}
package org.algorithms.strategy.greedyandknapsack;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Scanner;
public class Inflearn09_03 {
static class Wedding{
int in;
int out;
Wedding(int in, int out){
this.in=in;
this.out=out;
}
}
public static void main(String[] args){
Scanner in=new Scanner(System.in);
int n=in.nextInt();
Wedding[] arr= new Wedding[n];
for(int i=0;i<n;i++){
arr[i]=new Wedding(in.nextInt(), in.nextInt());
}
Inflearn09_03 main = new Inflearn09_03();
System.out.println(main.solution(arr));
}
public int solution(Wedding[] arr){
int answer=0;
int result=0;
Arrays.sort(arr, (o1, o2) -> (o1.in==o2.in)?o1.out-o2.out:o1.in-o2.in);
PriorityQueue<Wedding> pq = new PriorityQueue<>((o1, o2) -> (o1.out-o2.out));
// for(Wedding w : arr){
// System.out.print("w.in = " + w.in+" "+w.out);
// System.out.println();
// }
//5, 14
//12, 15
//14, 18
//15, 20
//20, 30
for(Wedding w : arr){
pq.offer(w);
// System.out.println("offer :" + w.in+" "+w.out);
while(!pq.isEmpty()){
if(pq.peek().out<=w.in){
Wedding w2=pq.poll();
// System.out.println("poll : "+w2.in+" "+w2.out);
}else break;
}
result = Math.max(pq.size(),result);
}
return result;
}
}'Java > Java 알고리즘 인프런' 카테고리의 다른 글
| [Ch.07 - Recursive] 01. 재귀함수 (0) | 2022.07.18 |
|---|---|
| [Ch.09 - Greedy] 04. 최대 수입 스케줄 (0) | 2022.07.18 |
| [Ch.09 - Greedy] 02. 회의실 배정 (0) | 2022.07.15 |
| [Ch.09 - Greedy] 01. 씨름 선수 (0) | 2022.07.15 |
| [리뷰] 해결 못한 알고리즘 다시 풀기 -2 (0) | 2022.07.08 |


