https://leetcode.com/problems/minimum-difficulty-of-a-job-schedule/
Minimum Difficulty of a Job Schedule - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
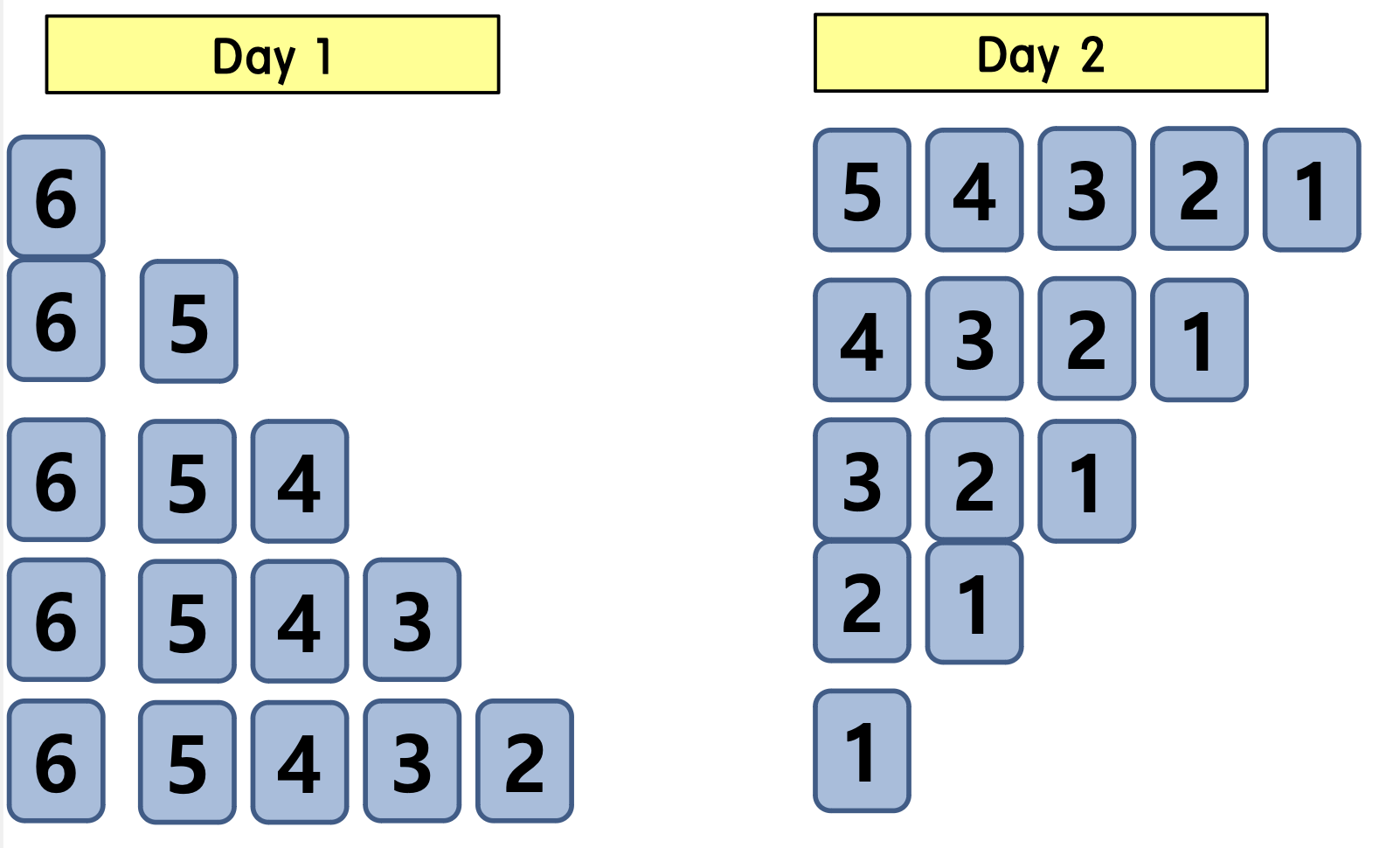
jobDifficulty ={6,5,4,3,2,1}, d=2
jobDifficulty ={7,1,7,1,7,1}, d=3

문제 분석

날짜들의 최솟값을 구하기 위해서는 각각의 날짜의 최곳값을 더해야한다.
-> DP로 구현

가능한 경우의 수 5가지
- 6+5 = 첫째 날의 최댓값 6, 두번째날의 최댓값 5
- 6+4= 첫째 날의 최댓값 6, 두번째날의 최댓값 4
- 6+3= 첫째 날의 최댓값 6, 두번째날의 최댓값 3
- 6+2= 첫째 날의 최댓값 6, 두번째날의 최댓값 2
- 6+1= 첫째 날의 최댓값 6, 두번째날의 최댓값 1
- 두번째날의 최댓값 : 두번째날이 가능한 경우의 수 중 가장 최솟값을 찾는다.
- 두번째날이 가능한 경우의 수를 차례대로 돌면서 Math.min찾기

날짜들의 최솟값을 구하기 위해서는 각각의 날짜의 최곳값을 더해야한다.
-> DP로 구현
가능한 경우의 수 4가지
- 7+7+1 = 첫째 날의 최댓값 7, 두번째날의 최댓값 7, 세번째날의 최댓값 1
- 7+1+7= 첫째 날의 최댓값 7, 두번째날의 최댓값 1, 세번째날의 최댓값 7
- 7+7+1= 첫째 날의 최댓값 7, 두번째날의 최댓값 7, 세번째날의 최댓값 1
- 7+1+7= 첫째 날의 최댓값 7, 두번째날의 최댓값 1, 세번째날의 최댓값 7
- 두번째날과 세번째날의 최댓값 : 두번째날과 세번째날이 가능한 경우의 수 중 가장 최솟값을 찾는다.
- 두번째날과 세번째날이 가능한 경우의 수를 차례대로 돌면서 Math.min찾기
문제 해결 순서
1. 주어진 작업들을 순서대로 날짜별로 최소한 하나의 작업이 수행되도록 나눈다.
2. 날짜의 값은 최고값이어야 한다.
3. 구한 날짜의 값의 합은 최솟값이 되어야 한다.
문제 구현 순서
1. 첫날 난이도가 높은 값으로 설정
2. 3중 For문
(1) DP를 날짜 순서대로 돈다
(2) DP를 순서길이대로 돈다
(3) DP를 순서길이부터 지금까지 돈만큼 확인해가면서 날짜별 최댓값과 날짜들의 최솟값 합을 찾는다.
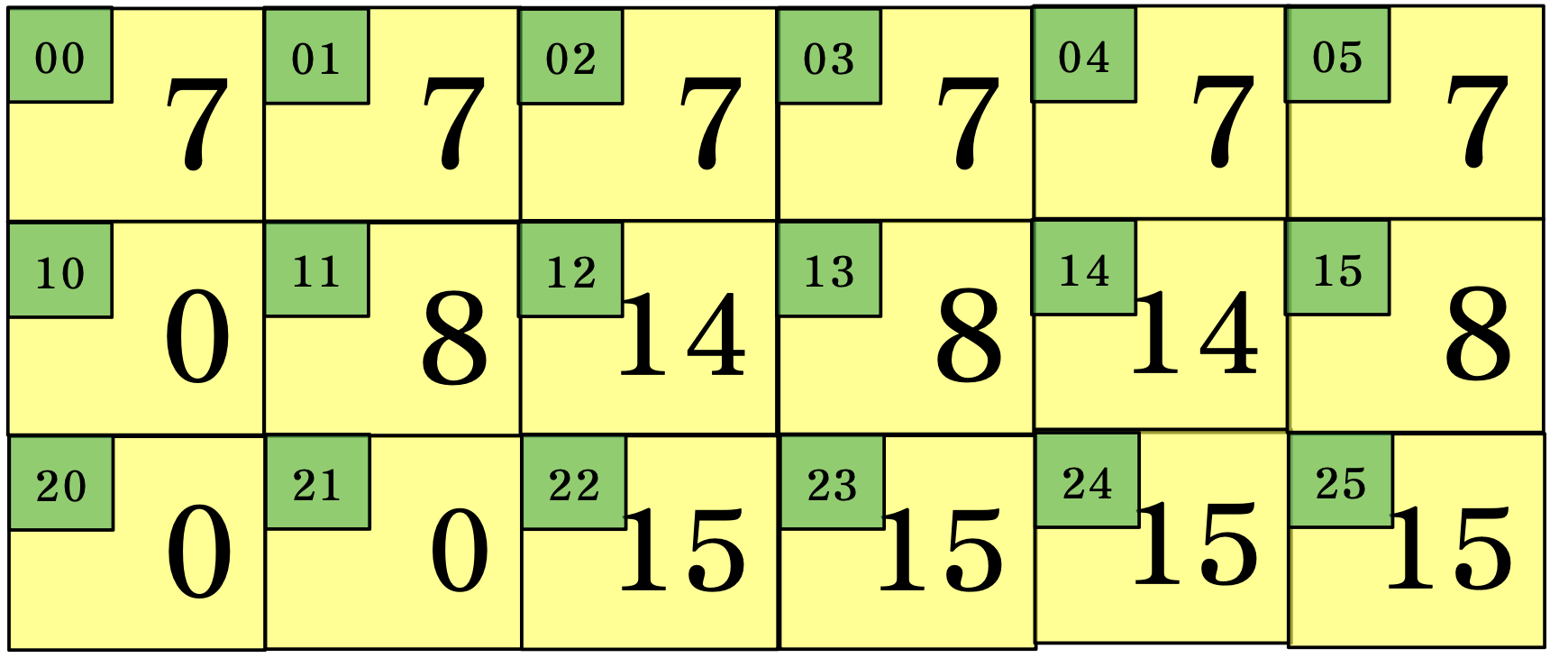
DP[i][j]는 해당 날짜의 순서길이에 해당하는 최솟값 배열
for (int d = 1; d < day; d++) {
for (int len = d; len < n; len++) { int localMax = jobDifficulty[len];
dp[d][len] = Integer.MAX_VALUE;
for (int schedule = len; schedule >= d; schedule--) {
localMax = Math.max(localMax, jobDifficulty[schedule]);
dp[d][len] = Math.min(dp[d][len], dp[d - 1][schedule - 1] + localMax);
} }
}
class Solution {
public int minDifficulty(int[] jobDifficulty, int day) {
//매일 최소 하나의 작업 완료
//각 날짜의 난이도는 최고난이도만 구하며, 전체 난이도 합은 최소가 되도록
int n = jobDifficulty.length;
if (n < day)return -1;
int[][] dp = new int[day][n];
dp[0][0] = jobDifficulty[0];
for (int i = 1; i < n; i++) {
dp[0][i] = Math.max(jobDifficulty[i], dp[0][i - 1]);
//System.out.println("dp[" + 0 + "][" + i + "]" + dp[0][i]);
}
for (int d = 1; d < day; d++) {
for (int len = d; len < n; len++) {
int localMax = jobDifficulty[len];
dp[d][len] = Integer.MAX_VALUE;
for (int schedule = len; schedule >= d; schedule--) {
//System.out.println("schedule: "+schedule);
//System.out.println("jobDifficulty[" + schedule + "] " + jobDifficulty[schedule]);
localMax = Math.max(localMax, jobDifficulty[schedule]);
//System.out.println("dp["+d+"]["+len+"]"+dp[d][len]);
//System.out.println("dp["+(d-1)+"]["+(schedule - 1)+"]"+dp[d - 1][schedule - 1]+"+"+localMax
// +"="+(dp[d - 1][schedule - 1] + localMax));
dp[d][len] = Math.min(dp[d][len], dp[d - 1][schedule - 1] + localMax);
//System.out.println("dp["+d+"]["+len+"]"+dp[d][len]);
}
//System.out.println("======schedule========");
//print(dp);
}
//System.out.println("======len========");
}
return dp[day - 1][n - 1];
}
public static void print(int[][] arr2) {
for (int i = 0; i < arr2.length; i++) {
for (int j = 0; j < arr2[i].length; j++) {
System.out.print("[" + i + "][" + j + "] " + arr2[i][j]);
}
System.out.println("");
}
}
}'Java > Java 알고리즘 LeetCode' 카테고리의 다른 글
| [LeetCode- Part. 4] 5. 이진 매트릭스 최단경로 (+BFS) (0) | 2022.11.13 |
|---|---|
| [LeetCode- Part. 4] 4. 최대 정사각형 # (+ 2차원 DP) (0) | 2022.11.13 |
| [LeetCode- Part. 4] 2. 슬라이딩 윈도우 최댓값 ##(+슬라이딩 윈도우, Deque) (1) | 2022.11.13 |
| [LeetCode- Part. 4] 1. N일 후 감옥 ## (+ 재귀함수, Arrays.toString, 삼항연산자) (1) | 2022.11.12 |
| [LeetCode- Part. 3] 5. Province의 수 (+DFS) (0) | 2022.11.12 |


