설명
가장 윗줄에 1부터 N까지의 숫자가 한 개씩 적혀 있다. 그리고 둘째 줄부터 차례대로 파스칼의 삼각형처럼 위의 두개를 더한 값이 저장되게 된다.
예를 들어 N이 4 이고 가장 윗 줄에 3 1 2 4 가 있다고 했을 때, 다음과 같은 삼각형이 그려진다.
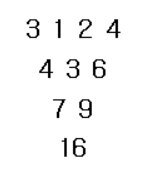
N과 가장 밑에 있는 숫자가 주어져 있을 때 가장 윗줄에 있는 숫자를 구하는 프로그램을 작성하시오.
단, 답이 여러가지가 나오는 경우에는 사전순으로 가장 앞에 오는 것을 출력하여야 한다.
입력
첫째 줄에 두개의 정수 N(1≤N≤10)과 F가 주어진다.
N은 가장 윗줄에 있는 숫자의 개수를 의미하며 F는 가장 밑에 줄에 있는 수로 1,000,000 이하이다.
출력
첫째 줄에 삼각형에서 가장 위에 들어갈 N개의 숫자를 빈 칸을 사이에 두고 출력한다.
답이 존재하지 않는 경우는 입력으로 주어지지 않는다.
예시 입력 1
4 16예시 출력 1
3 1 2 4파스칼의 삼각형 -> 다항식의 계수 -> 피보나치 수열
| 1 | 1 |
| 1 1 | 1C0 + 1C1 |
| 1 2 1 | 2C0 + 2C1 + 2C2 |
| 1 3 3 1 | 3C0 + 3C1 + 3C2 + 3C3 |
| 1 4 6 4 1 | 4C0 + 4C1 + 4C2 + 4C3 + 4C4 |
| 1 5 10 10 5 1 | 5C0 + 5C1 + 5C2 + 5C3 + 5C4 + 5C5 |
| 1 6 15 20 15 6 1 | 6C0 + 6C1 + 6C2 + 6C3 + 6C4 + 6C5 + 6C6 |
다항식 계수를 구하는 함수 combi
public int combi(int n, int r) {
if (dy[n][r] > 0)
return dy[n][r];
if (n == r || r == 0)
return 1;
else
return dy[n][r] = combi(n - 1, r - 1) + combi(n - 1, r);
}

| 1 3 3 1 | 3C0 + 3C1 + 3C2 + 3C3 |
| 1 2 1 | 2C0 + 2C1 + 2C2 |
| 1 1 | 1C0 + 1C1 |
| 1 | 1 |
DFS 종료 조건 :
a*1 + b*3 c*3 + d*1 = 16일 때,
if(flag) return;
if(L==n) {
if(sum==f){
for(int x : p) System.out.print(x+" ");
flag=true;
}
즉, N이 4이므로, a * 3C0 + b * 3C1 + c * 3C2 + d * 3C3 = 16이 성립하는 int 배열인 a []를 구하는 것
public void DFS (int L, int sum){
if(flag) return;
if(L==n) {
if(sum==f){
for(int x : p) System.out.print(x+" ");
flag=true;
}
}
else{
for(int i=1; i<=n; i++){
if(ch[i]==0){
ch[i]=1;
p[L]=i;
DFS(L+1, sum+(p[L] * b[L]));
ch[i]=0;
}
}
}
}16이 성립 되기 전까지는,
1부터 n까지 반복하면서, 체크 배열에 비어있을 경우 -> 체크 배열에 채우면서, 직접 i를 증가시켜가면서 확인한다.
ch[i]=1;
p[L]=i;
DFS(L+1, sum+(p[L] * b[L]));
ch[i]=0;-> 체크 배열에 i번째 체크를 한 후, i번째가 성립되지 않는다면 다시 i번째의 체크를 해제한다.
import java.util.*;
class Main {
static int[] b, p, ch;
static int n, f;
boolean flag = false;
int[][] dy = new int[35][35];
public int combi(int n, int r) {
if (dy[n][r] > 0)
return dy[n][r];
if (n == r || r == 0)
return 1;
else
return dy[n][r] = combi(n - 1, r - 1) + combi(n - 1, r);
}
public void DFS(int L, int sum) {
if (flag)
return;
if (L == n) {
if (sum == f) {
for (int x : p)
System.out.print(x + " ");
flag = true;
}
} else {
for (int i = 1; i <= n; i++) {
if (ch[i] == 0) {
ch[i] = 1;
p[L] = i;
DFS(L + 1, sum + (p[L] * b[L]));
ch[i] = 0;
}
}
}
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
n = kb.nextInt();
f = kb.nextInt();
b = new int[n];
p = new int[n];
ch = new int[n + 1];
for (int i = 0; i < n; i++) {
b[i] = T.combi(n - 1, i);
}
T.DFS(0, 0);
}
}
(1) 조합 구하는 함수를 이용해 b[i]를 구하기
(2) 조합 구하는 함수, DFS 함수
(3) ch배열은 m+1개의 길이를 갖는다.
: ch[i]==0일 때, 채우는데 ch[i]=1로 바꾼 후, DFS 돌리고 다시 ch[i]=0으로 설정
: a[i]의 경우에는 nC0+nC1+nC2+nC3순서로 i를 대입해준다.
import java.util.Scanner;
public class Main {
static int n,m;
static int[] a,b,ch;
static int[][] dy=new int[35][35];
static boolean flag=false;
public static void main(String[] args){
Scanner in=new Scanner(System.in);
n = in.nextInt();
m = in.nextInt();
a=new int[n];
b=new int[n];
ch=new int[n+1];
for(int i=0;i<n;i++){
b[i]=combi(n-1, i);
}
DFS(0,0);
}
static int combi(int n, int r){
if(dy[n][r]>0) return dy[n][r];
else{
if(n==r||r==0){
return 1;
}
else{
return dy[n][r]=combi(n-1,r)+combi(n-1,r-1);
}
}
}
static void DFS(int L, int sum){
if(flag) return;
if(L==n){
if(sum==m){
for(int x:a) System.out.print(x+" ");
flag=true;
}
}else{
for(int i=1;i<=n;i++){
if(ch[i]==0){
ch[i]=1;
a[L]=i;
DFS(L+1, sum+(a[L]*b[L]));
ch[i]=0;
}
}
}
}
}
'Java > Java 알고리즘 인프런' 카테고리의 다른 글
| [Ch.08 - DFS] 12. 미로탐색 (0) | 2022.07.30 |
|---|---|
| [Ch.08 - DFS] 11. 조합 구하기 (0) | 2022.07.30 |
| [Ch.08 - DFS] 09. 조합의 경우수(메모이제이션) (0) | 2022.07.29 |
| [Ch.08 - DFS] 08. 순열 구하기 (0) | 2022.07.29 |
| [Ch.08 - DFS] 07. 동전교환 # (1) | 2022.07.29 |

