1. 인덱스 구조 및 탐색
2. 인덱스 기본 사용법
3. 인덱스 확장기능 사용법
인덱스 구조 (일반적인 DBMS의 인덱스는 B*트리)
: 어떤 값으로 탐색하더라도 인덱스 루트에서 리프 블록까지 도달하기까지 읽는 블록 수가 같은 트리
B 트리, B+ 트리, B* 트리는 모두 데이터베이스나 파일 시스템에서 사용되는 인덱스 구조로, 데이터를 효율적으로 검색하고 관리하는 데에 활용됩니다. 각각의 트리는 특정한 용도나 성능 특성에 따라 설계되었으며, 목표하는 기능과 성능을 달성하기 위해 트리의 구조와 동작 방식에 차이가 있습니다. 이제 각 트리의 특징과 차이를 살펴보겠습니다.
1. B 트리 (B-Tree)
- B 트리는 여러 자식을 가지는 자가 균형 이진 트리로, 각 노드에는 키와 그에 대응하는 자식 노드를 저장합니다.
- 모든 리프 노드는 같은 레벨에 있으며, 트리의 높이가 균등하게 유지됩니다.
- B 트리는 디스크 I/O를 줄이고 효율적으로 데이터를 관리하기 위해 설계되었으며, 데이터베이스나 파일 시스템에서 널리 사용됩니다.
2. B+ 트리 (B+ Tree)
- B+ 트리는 B 트리의 변형으로, 리프 노드에만 데이터를 저장하고 내부 노드는 키만을 저장합니다.
- 모든 리프 노드는 연결 리스트로 연결되어 있어 범위 검색에 용이합니다.
- B+ 트리는 범위 검색이나 순차 접근에 특히 유용하며, 데이터베이스의 주요 인덱스 구조로 사용됩니다.
3. B* 트리 (B* Tree)
- B* 트리는 B+ 트리의 확장된 버전으로, 내부 노드에서도 분할이 발생할 수 있어 더 빈번한 리밸런싱이 일어납니다.
- B* 트리는 B+ 트리보다 더 높은 확장성과 성능을 제공하지만, 추가적인 분할과 병합이 발생하므로 구현이 더 복잡합니다.
- 일반적으로 B* 트리는 특별한 경우에 사용되며, 일반적인 상황에서는 B+ 트리가 더 많이 사용됩니다.
따라서 각각의 트리는 자료구조의 특징과 성능 특성에 따라 선택되며, 적절한 상황에서 사용됩니다. B+ 트리는 범위 검색에 더 효율적이며, B* 트리는 더 높은 확장성을 제공합니다. B 트리는 널리 사용되는 일반적인 인덱스 구조로서, 디스크 기반의 데이터베이스나 파일 시스템에서 효율적으로 사용됩니다.
그래프와 트리 (트리는 특별한 그래프 구조)
1. 계층 구조 vs. 네트워크 구조
- 트리는 계층적인 구조를 가지고 있습니다. 각 노드는 하나의 부모 노드와 여러 개의 자식 노드를 가질 수 있습니다. 루트에서부터 잎으로 향하는 방향성이 있습니다.
- 그래프는 네트워크 형태의 구조를 가지고 있습니다. 노드 간에 직접적인 관계가 있는 경우도 있고, 사이클이 발생할 수 있습니다.
2. 루트와 방향성
- 트리는 하나의 루트 노드를 가지며, 각 노드는 부모와 자식 노드 간의 관계가 있습니다. 루트에서 잎으로 향하는 방향성이 있습니다.
- 그래프는 루트 노드가 없고, 노드 간의 관계가 방향성을 가지지 않을 수도 있습니다.
3. 사이클의 존재 여부
- 트리는 사이클이 존재하지 않습니다. 즉, 트리에서 어떤 노드를 시작점으로 하여 임의의 경로를 따라가더라도 같은 노드를 두 번 이상 방문할 수 없습니다.
- 그래프는 사이클이 존재할 수 있습니다. 즉, 두 개의 노드 간에 경로가 있고 이 경로가 또 그 두 노드로 되돌아오는 경우를 말합니다.
4. 계층 구조의 표현
- 트리는 계층 구조를 표현하는 데 사용됩니다. 예를 들어, 파일 시스템이나 조직도를 표현하는 데에 사용됩니다.
- 그래프는 네트워크 구조를 표현하는 데 사용됩니다. 예를 들어, 도로망이나 소셜 네트워크 그래프를 표현하는 데 사용됩니다.
트리는 특정한 형태의 그래프로 볼 수 있지만, 그래프는 보다 일반적인 개념으로 더 다양한 형태의 구조를 포함합니다. 따라서 트리는 그래프의 특별한 경우라고 볼 수 있습니다.
이진트리 특징
이진 트리(Binary Tree)는 각 노드가 최대 두 개의 자식을 가질 수 있는 트리 구조입니다. 이진 트리는 다음과 같은 특징을 가지고 있습니다:
1. **계층적 구조**: 이진 트리는 계층적인 구조를 가지고 있습니다. 각 노드는 최대 두 개의 자식 노드를 가질 수 있으며, 각 자식 노드는 또 다시 최대 두 개의 자식을 가질 수 있습니다.
2. **루트(root) 노드**: 이진 트리는 하나의 루트 노드를 가집니다. 루트 노드는 트리의 최상위 노드로서 다른 모든 노드는 루트 노드로부터 직간접적으로 연결됩니다.
3. **부모(parent)와 자식(child) 노드**: 각 노드는 최대 두 개의 자식 노드를 가질 수 있습니다. 부모 노드는 자식 노드를 가리키며, 자식 노드는 부모 노드에 대한 참조를 가집니다.
4. **이진 트리의 종류**: 이진 트리에는 다양한 종류가 있습니다. 예를 들어, 완전 이진 트리(Complete Binary Tree), 이진 탐색 트리(Binary Search Tree), AVL 트리(AVL Tree), 레드-블랙 트리(Red-Black Tree) 등이 있습니다. 각각의 종류는 특정한 조건을 만족시키며 특별한 용도로 사용됩니다.
5. **이진 트리의 순회**: 이진 트리의 모든 노드를 방문하는 방법에는 세 가지 주요한 방법이 있습니다. 전위 순회(Preorder Traversal), 중위 순회(Inorder Traversal), 후위 순회(Postorder Traversal)입니다. 이러한 순회 방법은 트리에서 데이터를 조회하거나 수정하는 데 사용됩니다.
이진 트리는 다양한 응용 분야에서 사용되며, 데이터의 저장, 검색, 정렬 등 다양한 작업에 활용됩니다. 이진 트리는 다른 트리 구조의 기반으로 사용되기도 하며, 알고리즘과 자료구조에서 중요한 개념 중 하나입니다.
탐색에서 이진트리를 사용하는 이유
이진 트리(Binary Tree)는 탐색(Search) 작업을 효율적으로 수행하기 위해 사용되는 자료 구조 중 하나입니다. 다음은 이진 트리를 탐색에 사용하는 이유를 자세히 설명한 것입니다:
1. **시간 복잡도**: 이진 트리에서의 탐색은 평균적으로 O(log n)의 시간 복잡도를 가집니다. 이는 트리의 높이에 비례하는 것으로, 트리의 노드 개수가 늘어나도 탐색 시간이 느리게 증가합니다. 이는 매우 큰 데이터 세트에서도 빠른 탐색을 가능하게 합니다.
2. **정렬된 데이터**: 이진 트리는 각 노드가 정렬된 상태로 유지됩니다. 이는 데이터에 대한 효율적인 검색을 가능하게 합니다. 이진 트리를 사용하면 데이터를 정렬된 상태로 저장하고 탐색할 수 있기 때문에, 이진 탐색(Binary Search)을 통해 효율적으로 원하는 데이터를 찾을 수 있습니다.
3. **분할 및 정복**: 이진 트리는 탐색 작업을 분할 및 정복(Divide and Conquer) 전략을 사용하여 수행합니다. 각 노드는 왼쪽 자식과 오른쪽 자식으로 나뉘며, 각 하위 트리는 독립적으로 탐색될 수 있습니다. 이는 전체 데이터를 작은 단위로 나누어 각각의 작은 문제로 쪼개고, 각각을 해결한 후 결과를 합치는 방식으로 효율적인 탐색을 가능하게 합니다.
4. **범위 검색**: 이진 트리를 사용하면 범위 검색(range search)을 효율적으로 수행할 수 있습니다. 이진 트리는 정렬된 상태로 데이터를 저장하기 때문에 범위 검색을 수행할 때 효율적으로 탐색할 수 있습니다. 예를 들어, 주어진 범위에 속하는 모든 노드를 찾는 등의 작업을 빠르게 수행할 수 있습니다.
5. **메모리 사용**: 이진 트리는 각 노드가 최대 두 개의 자식 노드만 가질 수 있기 때문에 메모리를 효율적으로 사용할 수 있습니다. 이는 인덱스의 크기를 작게 유지하면서도 효율적인 검색을 제공하는 데 도움이 됩니다.
이러한 이유로 이진 트리는 데이터 검색을 위한 강력한 도구로 활용되며, 데이터베이스 시스템, 검색 엔진, 정렬 알고리즘 등 다양한 응용 분야에서 널리 사용됩니다.
범위 스캔을 위한 인덱스
(인덱스 스캔 시작지점을 찾아서 데이터를 탐색한다. -> 수직적 탐색 이후 수평적 탐색 진행)
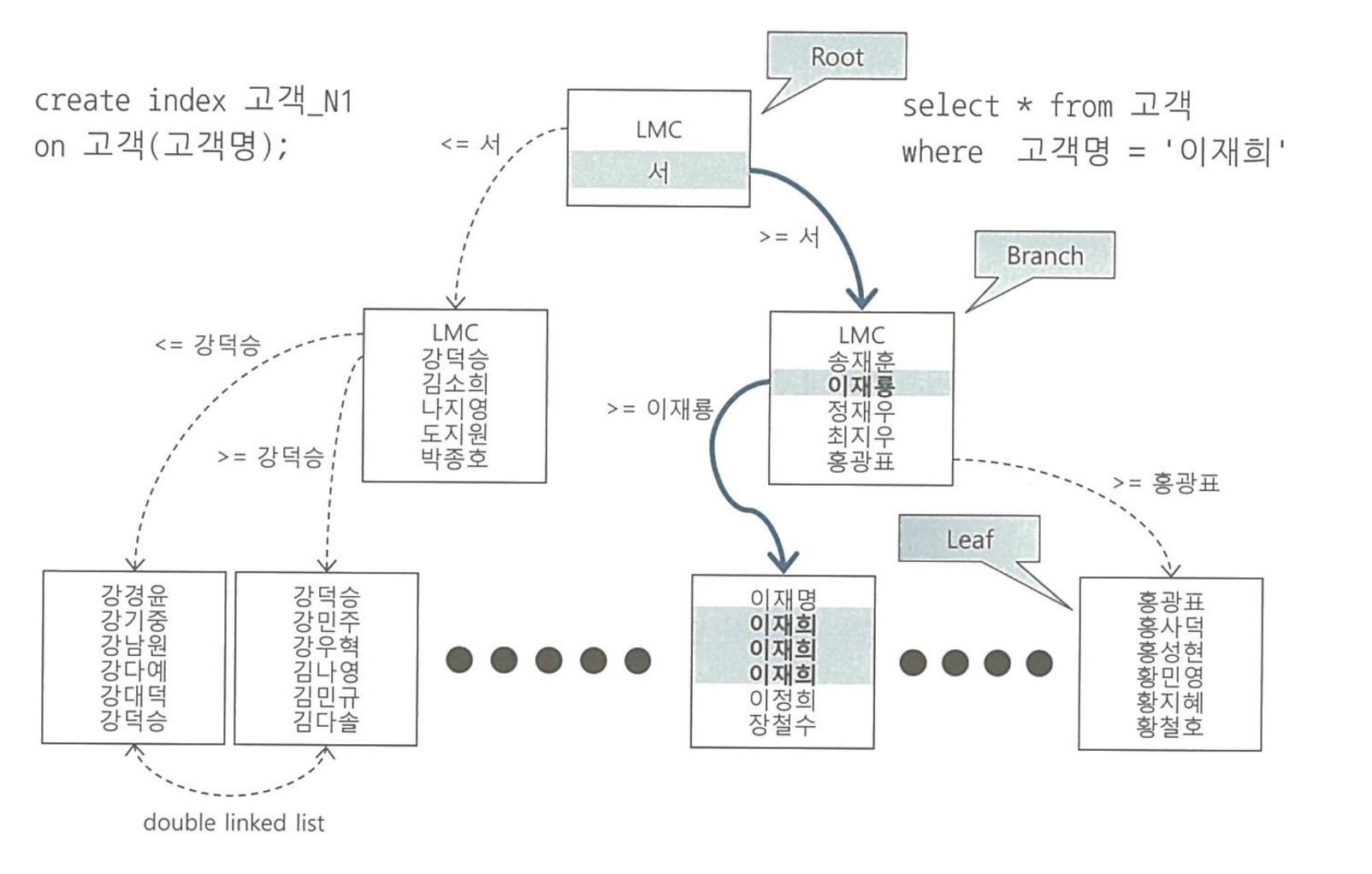
루트와 브랜치 블록에 있는 각 레코드는 하위 블록에 대한 주소값을 가진다.
: 키값은 하위 블록 키값의 범위를 나타내며, 루트와 브랜치 블록에는 키값을 갖지 않는 레코드 LMC가 존재 (가장 왼쪽 자식)
-> 키값을 가진 첫 번째 레코드보다 작거나 같은 레코드가 저장되어 있어서 이를 통해 최소값을 찾거나 특정 범위 내의 레코드를 검색하는 데 사용
리프 블록의 각 레코드는 정렬되어 있으며 해당 레코드의 ROWID를 통해 테이블 레코드를 찾아간다.
-> ROWID는 데이터 블록 주소 + 로우번호이므로 이를 이용해 블록에 접근해 블록 내 특정 레코드를 직접 찾는다.
1) 수직적 탐색
: 인덱스 스캔 시작지점 찾기 (조건을 만족하는 첫 번째 레코드)
루트에서 리프 블록까지 수직적 탐색 진행 (하위 블록에 대한 주소값을 통해 탐색)
-> 가장 왼쪽 자식과 찾고자 하는 값보다 크거나 같은 값을 찾을 때까지 하위블록으로 이동
브랜치 블록에서 원하는 레코드보다 큰 레코드를 찾은 경우 직전 레코드가 가리키는 하위블록으로 이동
-> 리프 블록에 도달했으므로 조건을 만족하는 첫 번째 레코드
(= 인덱스 스캔 시작지점으로 조건을 만족하는 첫 번째 레코드)
2) 수평적 탐색
: 찾고자 하는 데이터가 더 안나타날 때까지 찾는다.
인덱스 리프 블록은 리프 블록끼리 서로 앞뒤 블록에 대한 주소값을 갖는다.
-> 양방향 연결리스트 구조-> 앞 뒤 블록을 찾을 수 있는 포인터를 갖는다.
-> 이를 통해 조건을 만족하는 모든 데이터를 찾을 수 있다. -> 정렬되어 있으므로 양 옆을 비교하는 것이 원하는 모든 데이터를 찾는 방법
하지만 인덱스가 원하는 모든 칼럼을 갖고 있지 않는 경우 존재
-> ROWID를 통해 테이블 액세스 수행
결합 인덱스 구조
인덱스 칼럼 순서에 따라 비교연산 횟수의 차이가 존재할 수 있지만,
칼럼 순서에 따라 일량의 차이는 존재하지 않는다.
-> 그 이유는 균형 트리이기 때문에, 어떤 값으로 탐색하더라도 인덱스 루트에서 리프 블록에 도달하기까지 읽는 블록수는 같다.
(즉, 루트로부터 모든 리프 블록까지의 높이는 항상 같다.)
+) B트리
B트리 특징
B-트리는 균형 트리(Balanced Tree)의 일종으로, 모든 리프 노드가 동일한 레벨에 위치하도록 설계되어 있습니다. 이러한 특성으로 인해 B-트리는 어떤 값으로 탐색하더라도 인덱스 루트에서 리프 블록에 도달하기까지 읽는 블록 수가 동일합니다. 이로 인해 칼럼 순서에 따라 일량의 차이는 존재하지 않게 됩니다.
여기서 중요한 포인트는 B-트리의 균형 특성입니다. B-트리의 균형 특성은 다음과 같은 규칙을 따릅니다:
1. 모든 리프 노드가 동일한 레벨에 위치한다: B-트리에서 모든 리프 노드는 트리의 최하위 레벨에 위치합니다. 즉, 모든 리프 노드의 깊이가 동일합니다.
2. 모든 내부 노드의 자식 수는 일정 범위 내에 있다: B-트리에서 내부 노드의 자식 수는 특정 범위 내에 있어야 합니다. 이 범위는 최소 차수(minimum degree)와 최대 차수(maximum degree) 사이에 정의됩니다. 이러한 제한은 트리가 균형을 유지하도록 보장합니다.
이러한 균형 특성으로 인해 B-트리에서 어떤 값으로 탐색하더라도 인덱스 루트에서 리프 블록에 도달하기까지 읽는 블록 수가 일정하게 유지됩니다. 따라서 B-트리에서는 칼럼 순서에 따라 비교연산 횟수의 차이가 존재할 수 있지만, 일량의 차이는 존재하지 않게 됩니다. 이는 모든 리프 블록까지의 높이가 항상 동일하기 때문입니다.
B*트리 특징
B* 트리는 B-트리의 확장된 형태로, B-트리와 유사한 구조를 가지고 있지만 몇 가지 특별한 특징을 가지고 있습니다. 이러한 특징으로 인해 B* 트리는 특정 작업에서 성능이 향상될 수 있습니다. 아래에서 B* 트리의 주요 특징과 이로 인한 성능 향상에 대해 설명하겠습니다:
1. 더 많은 키 값 저장: B* 트리는 각 노드에서 더 많은 키 값을 저장할 수 있습니다. B-트리에서는 노드가 가득 찼을 때 분할을 수행하지만, B* 트리에서는 노드가 가득 차도 키 값을 재배치하여 공간을 활용합니다. 이로 인해 키 값들이 더 밀집되어 저장되며, 적은 레벨에서 더 많은 키를 저장할 수 있습니다.
2. 더 적은 레벨의 깊이: B* 트리는 더 많은 키 값을 저장할 수 있기 때문에 동일한 양의 데이터를 처리할 때 더 적은 수의 레벨이 필요합니다. 이는 탐색 및 삽입, 삭제 작업에 있어서 더 적은 I/O 비용을 발생시키므로 성능이 향상될 수 있습니다.
3. 불필요한 분할 최소화: B* 트리는 노드가 가득 찼을 때 바로 분할을 수행하지 않고, 일정한 수준 이상의 키 값이 모이면 분할을 수행합니다. 이는 불필요한 분할을 최소화하고 트리의 균형을 유지하는 데 도움이 됩니다.
4. 최적화된 탐색 경로: B* 트리는 더 적은 수의 레벨을 가지고 있기 때문에 탐색 경로가 최적화됩니다. 이는 탐색 작업에 있어서 더 빠른 속도를 제공할 수 있습니다.
5. 더 빠른 범위 탐색: B* 트리는 더 밀집된 구조를 가지고 있어서 범위 탐색 작업에 특히 유리합니다. 연속적인 키 값들이 더 빠르게 찾아지기 때문에 범위 탐색 작업에 있어서 더 효율적입니다.
이러한 특징들로 인해 B* 트리는 특정 작업에 있어서 더 뛰어난 성능을 제공할 수 있습니다. 특히 데이터베이스 시스템에서 인덱스 구조로 사용될 때, 데이터베이스 쿼리의 실행 속도를 향상시킬 수 있으며, 데이터의 삽입 및 삭제 작업에 있어서도 더 효율적으로 처리할 수 있습니다.
인덱스 구조에서 B*트리를 사용하는 이유
B* 트리는 B-트리의 변형으로, B-트리에서 발생할 수 있는 빈 공간의 낭비를 줄이고 검색 성능을 향상시키는 것을 목표로 합니다. 이를 위해 B* 트리는 B-트리와 다르게 리프 노드 사이에서도 다수의 연속적인 포인터를 가지고 있습니다.
B* 트리의 주요 특징과 이로 인한 이점은 다음과 같습니다:
1. 리프 노드의 가득 찬 상태 유지: B* 트리에서는 리프 노드의 가득 찬 상태를 유지하는 것이 중요합니다. 이를 위해 B* 트리는 리프 노드의 빈 공간을 최소화하고, 데이터의 삽입 및 삭제 시에도 리프 노드의 재배치를 통해 최적화된 구조를 유지합니다. 이는 빈 공간을 줄여 검색 성능을 향상시키는데 도움이 됩니다.
2. 더 적은 레벨의 트리: B* 트리는 더 많은 포인터를 가진다는 점에서 B-트리보다 더 적은 레벨의 트리를 유지할 수 있습니다. 이는 탐색 시에 필요한 디스크 I/O 횟수를 줄여 성능을 향상시킵니다.
3. 더 효율적인 범위 검색: B* 트리는 범위 검색(특정 값 사이의 범위에서 데이터를 검색하는 것)에 더 효율적입니다. 연속적인 리프 노드 사이의 포인터를 통해 범위 검색을 빠르게 수행할 수 있습니다.
4. 공간 사용 최적화: B* 트리는 B-트리보다 더 효율적으로 공간을 사용합니다. 빈 공간의 최소화와 더 많은 포인터를 통해 공간의 낭비를 줄이고 인덱스의 크기를 최적화할 수 있습니다.
이러한 이유로 B* 트리는 B-트리보다 더 성능이 우수하며, 특히 범위 검색과 같은 연산에서 더 효율적입니다. 따라서 데이터베이스에서는 B* 트리를 더 많이 사용하여 인덱스 구조를 최적화하는 경향이 있습니다.
인덱스를 사용하는 이유
: 일정 범위만 스캔하기 위해서
일정 범위만 스캔하기 위해서 필요한 조건
:스캔 시작점과 끝지점
가공한 값이나 중간값 찾을 때
-> 스캔 시작점을 찾을 수 없고 멈출 수도 없음
-> 리프 블록 전체 스캔하는 색인 전체 스캔 필요 (Index Full Scan)
"색인 전체를 스캔한다"는 말은 주로 인덱스에 조건으로 사용된 칼럼이 없어서 인덱스의 모든 키를 확인하면서 조건에 부합하는 행을 찾는 것을 의미합니다.
예를 들어, WHERE 절에 사용된 조건이 인덱스의 키 칼럼이 아닌 경우에는 인덱스를 사용하여 특정한 레코드를 찾을 수 없습니다. 따라서 데이터베이스는 인덱스의 모든 키를 확인하면서 조건에 부합하는 행을 찾아야 합니다. 이 과정에서 인덱스의 전체를 스캔하게 되며, 이러한 작업을 "색인 전체를 스캔한다"고 표현합니다.
이러한 경우에는 인덱스를 사용하여 데이터를 검색하는 것보다는 테이블의 전체를 스캔하는 것이 더 효율적일 수 있습니다. 인덱스를 사용하여 조건에 부합하는 행을 찾지 못하고 테이블의 전체를 스캔해야 하기 때문에 인덱스의 유용성이 크게 감소하게 됩니다. 따라서 데이터베이스 시스템은 인덱스를 효율적으로 활용하여 쿼리를 최적화하는 것이 중요합니다.
Index Range Scan을 하지 않는 경우
- substr, nvl, like, or ,in 연산
단, OR과 IN 연산의 경우 다음과 같이 힌트를 주어 유도 가능
OR Expansion
- Union All로 옵티마이저가 변환한다.
- use_concat 힌트로 실행계획을 유도할 수 있다.
IN-List Iterator
- 개수만큼 Index Ragne Scan 반복
- Union All로 변환한 것과 같다.
Index Range Scan을 하는 경우
- 인덱스 선두 칼럼이 가공하지 않는 상태로 조건절에 있는 경우
인덱스를 탄다.
-> 인덱스 범위 탐색을 한다.
-> 인덱스 범위 탐색을 하면 항상 성능이 좋을까?
- 인덱스 범위 탐색을 하는 이유
- 스캔 범위를 줄이기 위해
- 인덱스를 잘 탔는지는 인덱스 리프 블록에서 스캔하는 양을 확인해야한다.
-> 인덱스 스캔 효율화
소트 연산 생략 + 부분 범위 탐색이 가능한 인덱스
1. 소트 연산 생략 (Avoidance of Sorting Operation)
- 데이터베이스에서 정렬 연산은 비용이 많이 드는 작업 중 하나입니다. ORDER BY 절이나 GROUP BY 절을 사용할 때 정렬이 필요하며, 대용량의 데이터를 정렬하는 과정은 시간과 자원을 많이 소모합니다.
- 인덱스를 사용하면 데이터를 정렬된 상태로 저장하기 때문에 정렬 작업을 추가로 수행하지 않고도 쿼리 결과를 반환할 수 있습니다. 즉, 인덱스를 사용하면 소트 연산을 생략할 수 있습니다.
2. 부분 범위 처리 (Partial Range Access)
- 인덱스를 사용하면 특정한 범위의 데이터에 빠르게 접근할 수 있습니다. 인덱스의 구조상 특정 범위의 데이터를 찾는 것이 효율적으로 가능하기 때문입니다.
- 따라서 WHERE 절에 조건이 포함된 쿼리를 수행할 때 인덱스를 사용하면 조건에 부합하는 데이터만을 처리할 수 있습니다. 이를 통해 전체 테이블을 스캔하는 대신 인덱스의 일부만을 스캔하여 필요한 부분 범위에 대한 처리를 할 수 있습니다.
인덱스 사용시 생략이 가능한 이유
- 결과 집합이 순번 순으로 출력 -> 실행 계획에 SORT ORDER BY 연산이 없음
- 인덱스 리프 블록은 양방향 연결 리스트
- 오름차순 : 조건을 만족하는 가장 작은 값 찾아서 수직적 탐색 -> 우측으로 수평적 탐색
- 내림차순 : 조건을 만족하는 가장 큰 값 찾아서 수직적 탐색 -> 좌측으로 수평적 탐색
소트 연산을 생략하지 못하게 하는 칼럼의 가공
1. ORDER BY 절에서의 칼럼의 가공
- 장비번호+변경일자+변경순번이 인덱스
- 인덱스 리프 블록 스캔시 -> 변경일자+변경순번으로 정렬
SELECT *
FROM 상태변경이력
WHERE 장비번호 = 'C'
ORDER BY 변경일자, 변경순번
-> 소트 연산 생략
SELECT *
FROM 상태변경이력
WHERE 장비번호 = 'C'
ORDER BY 변경일자 || 변경순번-> 소트 연산 생략 불가
- 주문일자+주문번호가 인덱스
SELECT *
FROM (
SELECT TO_CHAR(A.주문번호, 'FM000000') AS 주문번호
,A.업체번호
,A.주문금액
FROM 주문 A
WHERE A.주문일자 = :dt
AND A.주문번호 > NVL( :next _ord_no , 0)
ORDER BY 주문번호
)
WHERE ROWNUM <= 30-> ORDER BY하는 주문번호가 TO_CHAR로 가공된 칼럼
SELECT *
FROM (
SELECT TO_CHAR(A.주문번호, 'FM000000') AS 주문번호
,A.업체번호
,A.주문금액
FROM 주문 A
WHERE A.주문일자 = :dt
AND A.주문번호 > NVL( :next _ord_no , 0)
ORDER BY A.주문번호
)
WHERE ROWNUM <= 30-> ORDER BY하는 주문번호는 인덱스가 사용된 칼럼
2. SELECT-LIST에서 칼럼 가공
- 장비번호+변경일자+변경순번이 인덱스
SELECT MIN(변경순번)
FROM 상태변경이력
WHERE 장비번호 = 'C'
AND 변경일자 = '20180316'SELECT MAX(변경순번)
FROM 상태변경이력
WHERE 장비번호 = 'C'
AND 변경일자 = '20180316'-인덱스 리프 블록은 양방향 연결 리스트
-> 최솟값 찾기 : LMC
-> 최댓값 찾기 : RMC
STATEMENT
SORT AGGREGATE
FIRST ROW
INDEX RANGE SCAN (MIN/MAX) 상태변경이력_PK
인덱스는 문자열 기준 = 가공여부를 판단하는 기준
SELECT NVL(MAX(TO_NUMBER(변경순번)),0)
FROM 상태변경이력
WHERE 장비번호 = 'C'
AND 변경일자 = '20180316'SELECT NVL(TO_NUMBER(MAX(변경순번)),0)
FROM 상태변경이력
WHERE 장비번호 = 'C'
AND 변경일자 = '20180316'-> 1) INDEX RANGE SCAN
-> 2) FIRST ROW INDEX RANGE SCAN (MIN/MAX)
SELECT 장비번호
,장비명
,상태코드
,(
SELECT MAX(변경일자)
FROM 상태변경이력
WHERE 장비번호 = P. 장비번호
) 최종변경일자
,(
SELECT MAX(변경순번)
FROM 상대변경이력
WHERE 창비번호 = P.장비번호
AND 변경일자 = (
SELECT MAX(변경일자)
FROM 상태변경이력
WHERE 장비번호 = P.장비번호
)
) 최종변경순번
FROM 장비 P
WHERE 장비구분코드 = 'A001'-> 상태변경이력 테이블을 여러번 읽는다.
-> PK 칼럼이 더 많아질수록 성능이 나빠짐
PK 칼럼이 많아져도 덜 복잡하도록 변경
SELECT 장비번호
,장비명
,상태코드
,SUBSTR(최종이력, 1, 8) 최종변경일자
,SUBSTR(최총이력, 9) 최총변경순번
FROM (
SELECT 장비번호
,장비명
,상태코드
,(SELECT MAX(변경일자||변경순번)
FROM 상대변경이력
WHERE 장비번호 = P.장비번호) 최종이력
FROM 장비 P
WHERE 장비구분코드 = 'A001'->인덱스 칼럼을 가공했으므로, 장비의 이력을 모두 읽는다.
-> Top N 알고리즘
위의 쿼리와 기존 쿼리를 비교하여 TOP-N 알고리즘에 대해 설명해드리겠습니다.
SELECT P.장비번호,
P.장비명,
P.상태코드,
A.최종변경일자,
B.최종변경순번
FROM 장비 P,
(SELECT 장비번호,
MAX(변경일자) AS 최종변경일자
FROM 상태변경이력
GROUP BY 장비번호) A,
(SELECT 장비번호,
MAX(변경순번) AS 최종변경순번
FROM 상대변경이력
WHERE (장비번호, 변경일자) IN (SELECT 장비번호,
MAX(변경일자) AS 최종변경일자
FROM 상태변경이력
GROUP BY 장비번호)
GROUP BY 장비번호) B
WHERE P.장비번호 = A.장비번호(+)
AND P.장비번호 = B.장비번호(+)
AND P.장비구분코드 = 'A001';
TOP-N 알고리즘은 쿼리의 결과에서 가장 크거나 작은 N개의 항목을 찾는데 사용됩니다. 이를 위해 서브쿼리나 조인 등을 활용하여 데이터를 검색하고 정렬하고 필요한 개수만큼의 결과를 반환합니다.
기존 쿼리는 서브쿼리를 사용하여 각각의 테이블에서 최대값을 찾고 있었습니다. 이는 서브쿼리를 통해 데이터를 여러 번 스캔하므로 성능에 부담이 될 수 있습니다.
변경된 쿼리는 JOIN과 서브쿼리를 사용하여 데이터를 한 번만 스캔하고 필요한 정보를 추출합니다. 이렇게 함으로써 데이터베이스 엔진은 효율적으로 쿼리를 실행할 수 있고 성능을 향상시킬 수 있습니다.
Top N 알고리즘
Top-N 알고리즘은 일반적으로 데이터에서 상위 N개의 결과를 찾는 데 사용됩니다. 이 알고리즘은 주로 다음과 같은 상황에서 사용됩니다:
1. 랭킹 또는 최상위 결과 필요
데이터에서 가장 높은 점수를 가진 항목, 가장 많이 판매된 상품, 또는 가장 활발한 고객 등과 같이 상위 N개의 결과가 필요한 경우에 사용됩니다.
2. 페이징
대용량 데이터 세트에서 결과를 페이징하여 사용자에게 표시할 때 사용됩니다. 예를 들어, 사용자에게 웹 검색 결과를 페이지 단위로 표시하려는 경우 상위 N개의 결과를 먼저 표시하고 사용자가 다음 페이지로 이동할 수 있게 합니다.
3. 통계 및 분석
데이터 분석에서 가장 빈도가 높은 값, 가장 큰 값 또는 가장 작은 값 등 특정 범주에 대한 상위 N개의 결과를 찾는 데 사용됩니다.
사용법
1. 정렬 후 잘라내기
전체 데이터를 정렬한 후 상위 N개의 결과를 선택합니다. 이 방법은 일반적으로 소량의 데이터에 대해서만 유용하며, 대용량 데이터에 대해서는 효율적이지 않을 수 있습니다.
2. 우선순위 큐
우선순위 큐를 사용하여 상위 N개의 결과를 유지합니다. 데이터가 추가될 때마다 우선순위 큐를 업데이트하고, 필요한 상위 N개의 결과를 추출합니다. 이 방법은 대용량 데이터에 대해서도 효율적으로 동작할 수 있습니다.
Top-N 알고리즘은 데이터베이스 쿼리나 데이터 처리 작업에서 자주 사용되며, 성능 향상과 사용자 경험 향상을 위해 중요한 역할을 합니다.
+) 인덱스 선두 칼럼의 중요성
인덱스에서 선두 칼럼은 검색 성능에 매우 중요한 역할을 합니다. 선두 칼럼은 인덱스의 첫 번째로 정의된 칼럼을 가리킵니다. 이 칼럼은 인덱스의 정렬 및 검색 기준이 되며, 쿼리 성능에 직접적인 영향을 미칩니다. 여러 가지 이유로 인해 선두 칼럼의 중요성이 강조됩니다.
1. **검색 효율성**: 선두 칼럼은 인덱스의 첫 번째로 정렬되어 있으므로, 해당 칼럼으로 검색할 때 인덱스 스캔을 효율적으로 수행할 수 있습니다. 인덱스 스캔은 원하는 데이터를 빠르게 찾을 수 있는 방법 중 하나이며, 선두 칼럼이 검색 조건에 포함되면 검색 성능이 크게 향상될 수 있습니다.
2. **쿼리 최적화**: 데이터베이스 쿼리 옵티마이저는 선두 칼럼을 사용하여 쿼리 실행 계획을 결정합니다. 선두 칼럼을 기준으로 데이터를 정렬하고 필터링하면 쿼리 최적화 과정에서 적절한 인덱스를 선택하여 효율적인 검색 계획을 수립할 수 있습니다.
3. **인덱스 이용도**: 선두 칼럼이 자주 사용되는 쿼리에서 사용되면 인덱스의 이용도가 높아집니다. 이는 데이터베이스가 인덱스를 효과적으로 활용하여 성능을 향상시킬 수 있는 중요한 요소입니다.
4. **인덱스 결합 및 범위 스캔**: 선두 칼럼을 기반으로한 인덱스 결합이나 범위 스캔에도 중요한 영향을 미칩니다. 선두 칼럼이 중요하지 않으면 인덱스 결합이나 범위 스캔을 수행할 때 인덱스의 이점을 충분히 활용할 수 없을 수 있습니다.
따라서 인덱스에서 선두 칼럼은 데이터베이스 성능 및 쿼리 최적화에 있어서 매우 중요한 역할을 합니다. 쿼리의 특성과 데이터 패턴을 고려하여 적절한 선두 칼럼을 선택하는 것이 중요합니다.
선두 칼럼 선정 기준
카디널리티는 선두 칼럼을 선택하는데 중요한 요소 중 하나일 수 있지만, 항상 결정적인 기준은 아닙니다. 카디널리티는 해당 칼럼의 고유한 값의 수를 나타내며, 값이 다양할수록 카디널리티가 높습니다. 일반적으로 카디널리티가 높은 칼럼은 인덱스에 적합한 선두 칼럼으로 간주될 수 있습니다. 왜냐하면 카디널리티가 높을수록 해당 칼럼을 이용한 검색이 데이터를 더 잘 필터링할 수 있기 때문입니다.
그러나 카디널리티만으로 선두 칼럼을 선택하는 것은 충분하지 않습니다. 다른 요소들도 고려되어야 합니다. 예를 들어:
1. **검색 패턴**: 어떤 종류의 쿼리가 자주 발생하는지에 따라 선두 칼럼을 선택해야 합니다. 가장 빈번하게 사용되는 조건으로 필터링되는 칼럼이 선두 칼럼으로 선택될 수 있습니다.
2. **조인 및 그룹화**: 조인 또는 그룹화 작업에서 선두 칼럼이 사용되는 경우가 있습니다. 이 경우 해당 칼럼을 선두 칼럼으로 선택하여 조인 또는 그룹화 성능을 최적화할 수 있습니다.
3. **데이터 패턴**: 데이터가 어떻게 분포되어 있는지에 따라 선두 칼럼을 선택해야 합니다. 예를 들어, 카디널리티가 높더라도 데이터가 균일하게 분포되어 있지 않는다면 선두 칼럼으로 선택되기 어려울 수 있습니다.
4. **쿼리 최적화**: 데이터베이스 옵티마이저가 쿼리 실행 계획을 수립할 때 고려되는 요소도 있습니다. 쿼리의 성능을 최적화하기 위해 선두 칼럼을 선택하는 방법은 데이터베이스 옵티마이저의 역할과 관련이 있습니다.
따라서 선두 칼럼을 선택할 때는 카디널리티뿐만 아니라 다양한 요소를 고려해야 합니다. 가장 효율적인 선두 칼럼을 선택하기 위해서는 실제 데이터와 쿼리 패턴을 분석하고 실험하여 결정해야 합니다.
자동 형변환으로 인한 테이블 전체 스캔 방지
: 조건절이 인덱스의 선두 칼럼이고, 따로 가공하지 않았는데 테이블 전체 스캔하는 경우
오라클의 경우
1) 숫자형과 문자형이 만날 경우 숫자형 칼럼 기준으로 문자형 칼럼을 변환한다.
(-> LIKE의 경우 문자열 비교 연산자이므로, 문자형 기준으로 숫자형 칼럼 변환)
2) 날짜형과 문자형이 만날 경우 날짜형 칼럼 기준으로 문자형 칼럼을 변환한다.
(-> 날짜형을 사용할 경우에는 날짜 포맷을 정확히 지정해주는 습관이 필요)
LIKE를 옵션 조건 처리 목적으로 사용할 때, 인덱스 스캔 효율에 영향을 미치는 경우
- 계좌번호 선택 입력
--SQL1 : 사용자가 계좌번호를 입력할 경우
SELECT * FROM 거래
WHERE 계좌번호 = :acnt _no AND 거래일자 bet ween : trd_dt 1 and : trd_dt 2
--SQL2 : 사용자가 계좌번호를 입력하지 않을 경우
SELECT * FROM 거래
WHERE 거래일자 between : trd_dt 1 and : trd_dt 2
1) 인덱스 전체 탐색
SELECT *
FROM 거래
WHERE 계좌번호 LIKE :acnt _no || '%'
AND 거래일자 between : trd_dt 1 and : trd_dt 22) 인덱스 범위 탐색
SELECT *
FROM 거래
WHERE (계좌번호 = :acnt_no OR :acnt_no IS NULL)
AND 거래일자 BETWEEN :trd_dt1 AND :trd_dt2;
자동 형변환으로 인한 에러
1) 실행 에러
- 숫자형 칼럼과 문자형 칼럼 비교시, 문자형 칼럼이 숫자형으로 변환
->변환 불가능한 문자열 입력시 에러 발생
2) 결과 오류
- DECODE 함수 처리시, 자동 형변환 규칙
- DECODE(a, b, c, d)에서 반환값의 데이터 타입은 c에 의해 결정되므로
1) c가 문자형이고 d가 숫자형이면 d는 문자형으로 변환
2) c가 null이면, VARCHAR2로 취급
select round(avg(sal)) avg_sal
,min(sal) min_sal
,max(sal) max_sal
,max(decode(job, 'PRESIDENT' , NULL, sal)) max_sal2
from emp;-> c가 NULL이므로, sal은 숫자형임에도 불구하고 VARCHAR2로 변환
-> 따라서 문자형과 숫자형을 비교 -> 문자열 기준으로 가장 큰 값 출력
NULL의 경우에도 데이터 타입 명시 필요
select round(avg(sal)) avg_sal
,min(sal) min_sal
,max(sal) max_sal
,max(decode(job, 'PRESIDENT' , TO_CHAR(NULL), sal)) max_sal2
from emp;-> 자동 형변환을 의존하지 않고, 인덱스 칼럼 기준으로 칼럼과 값을 형변환 필요
+) TABLE FULL SCAN vs INDEX FULL SCAN
TABLE FULL SCAN이 INDEX FULL SCAN보다 좋은 경우
1. 데이터 양이 적은 경우:
테이블의 전체 데이터 양이 매우 적을 때는 인덱스를 사용하여 데이터를 찾는 것보다 테이블 전체를 스캔하는 것이 더 효율적입니다. 이는 인덱스를 사용하는 오버헤드를 줄여 성능을 향상시킬 수 있습니다.
2. 검색 조건이 포함되지 않은 경우
쿼리에 검색 조건이 없거나, 검색 조건이 전체 데이터를 대상으로 하는 경우에는 인덱스를 사용하는 것보다 테이블 전체를 스캔하는 것이 더 효율적입니다. 인덱스를 사용하는 경우 추가적인 비용이 발생하므로, 검색 조건이 없는 경우에는 테이블 전체를 스캔하는 것이 더 효율적입니다.
3. 인덱스의 카디널리티가 낮은 경우
인덱스의 카디널리티가 낮아서 인덱스를 사용하여 데이터를 검색하는 것보다 테이블 전체를 스캔하는 것이 더 효율적인 경우가 있습니다. 카디널리티가 낮은 인덱스는 중복된 값이 많아서 인덱스를 사용하는 것이 오히려 추가적인 오버헤드를 발생시킬 수 있습니다.
4. 접근할 데이터가 매우 넓은 범위에 분포되어 있는 경우
검색할 데이터가 인덱스의 키 값으로 연속적으로 분포되어 있지 않고, 여러 블록에 걸쳐있는 경우에는 테이블 전체를 스캔하는 것이 더 효율적일 수 있습니다. 인덱스를 사용하는 경우 여러 블록을 읽어야 하므로 추가적인 I/O 비용이 발생할 수 있습니다.
대부분의 경우에는 INDEX FULL SCAN이 TABLE FULL SCAN보다 더 효율적
이는 인덱스를 사용하여 데이터를 검색하는 것이 일반적으로 테이블을 전체적으로 스캔하는 것보다 더 빠르기 때문입니다.
1. 데이터 양이 큰 경우
데이터 양이 많은 경우에는 인덱스를 사용하여 데이터를 검색하는 것이 더 빠릅니다. 인덱스는 특정 조건에 맞는 데이터를 빠르게 찾을 수 있도록 키 값으로 정렬되어 있기 때문에, 인덱스를 사용하면 필요한 데이터에 빠르게 접근할 수 있습니다.
2. 검색 조건이 있는 경우
쿼리에 검색 조건이 포함된 경우에는 인덱스를 사용하여 검색하는 것이 더 효율적입니다. 인덱스를 사용하면 필요한 데이터만을 선택적으로 읽을 수 있기 때문에 검색 조건에 해당하는 데이터를 빠르게 찾을 수 있습니다.
3. 인덱스의 카디널리티가 높은 경우
인덱스의 카디널리티가 높으면 인덱스를 사용하여 데이터를 검색하는 것이 더 효율적입니다. 카디널리티가 높은 인덱스는 중복된 값이 적고, 각 값에 대한 인덱스 엔트리가 분산되어 있기 때문에 더 정확하고 효율적인 검색이 가능합니다.
따라서 대부분의 경우에는 인덱스를 사용하여 데이터를 검색하는 것이 더 효율적입니다. 그러나 데이터의 분포나 쿼리의 성격에 따라서는 TABLE FULL SCAN이 더 나은 선택일 수도 있습니다. 종종 이 둘을 혼합하여 사용하는 것이 최적의 성능을 얻을 수 있는 방법일 수 있습니다.
'Data Science > SQLP' 카테고리의 다른 글
| 1. SQL 처리 과정과 I/O (2) | 2024.03.23 |
|---|---|
| SQLP 과목 변경 (1) | 2023.10.07 |
| [SQL] 프로그래머스 SQL (0) | 2022.10.14 |
| [기술면접 대비] DB 내용 정리 (회복전까지) (0) | 2022.06.25 |
| [ORACLE] 트리거 만들기 (0) | 2022.05.02 |


